본 포스트에서는 confusion matrix를 matplotlib.pyplot 라이브러리를 사용하여 직접 구현해 볼 것입니다.
seaborn 라이브러리를 사용하면 훨씬 쉽고 빠르게 구현할 수 있지만, 내부 원리를 정확히 공부하기 위해 seaborn은 사용하지 않겠습니다.
라이브러리 가져오기
from sklearn.metrics import confusion_matrix # confusion matrix 계산
from sklearn.metrics import accuracy_score # accuracy 계산
from sklearn.metrics import classification_report # 각 성능지표에 대한 분류 보고서 출력
confusion matrix의 출력 방식을 확인해보기 위해 먼저 사이킷런의 confusion matrix 라이브러리를 한번 사용해보겠습니다.
y_actual = [1,1,0,1,0,0,1,0,0,0]
y_pred = [1,0,0,1,0,0,1,1,1,0]
CM = confusion_matrix(y_actual, y_pred)
print('Confusion Matrix = \n', CM)
confusion matrix를 만들기 위해서는 y_actual과 y_pred가 필요합니다. 이 두 가지 배열을 넣어주면 confusion matrix() 함수가 TP, TN, FP, FN을 계산해줍니다.
그런데 위 결과만 봐서는 어떤 숫자가 어떤 항목에 해당하는지 잘 모르겠죠? 결과는 아래 그림처럼 해석하면 됩니다.
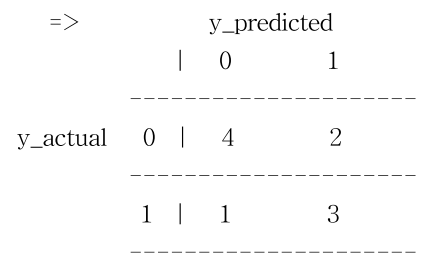
FP=2, TP=3, TN=4, FN=1으로 해석할 수 있습니다.
이제 원리를 알았으니 본격적으로 예쁘게 시각화하는 코드를 작성해보도록 하겠습니다.
Confusion matrix 시각화 함수 정의
import matplotlib.pyplot as plt
import numpy as np
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
'''
본 함수는 confusion matrix를 그려준다.
Normalization은 normalize=True로 바꾸면 적용된다.
'''
import itertools
if normalize:
# 행 단위로 정규화 : 클래스에 대한 예측의 비율을 구할 수 있음
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print('Normalized confusion matrix')
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap) # 원하는 사이즈의 픽셀을 원하는 색으로 채운 그림 생성
plt.title(title)
plt.colorbar() # confusion matrix의 값에 해당하는 색상 표시
tick_marks = np.arange(len(classes)) # 클래스 개수에 해당하는 값들로 구성된 배열 생성
plt.xticks(tick_marks, classes, rotation=45) # x축 눈금 레이블 45도로 회전해서 표시
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd' # normalization이 True인 경우 소수점 둘째 자리까지 표시, 아니면 정수 형태
thresh = cm.max() / 2. # 텍스트 색상 결정하기 위한 임계값 설정 (최대값/2)
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])): # i는 행, j는 열 인덱스
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment='center', # 텍스트를 셀 중앙에 배치
color='white' if cm[i, j] > thresh else 'black') # 해당 셀 값이 임계값보다 크면 흰색, 작으면 검은색
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout() # subplot들이 서로 겹치지 않게 최소한의 여백을 만들어줌
본 포스트에서는 정규화를 하지 않을 것이지만, 일단은 정규화를 할 경우까지 생각해서 구현해보았습니다. 그래도 일반적인 경우 정규화는 하지 않기 때문에 defualt는 normalize=False 입니다.
텍스트 색상의 경우에는 바탕색이 어두울 때 텍스트까지 검정색이면 텍스트가 전혀 보이지 않을 수 있기 때문에, 임계 값을 정해두고 바탕색이 밝으면 텍스트는 검정색, 바탕색이 어두우면 텍스트는 흰색으로 나타나게 만들었습니다.
시각화
cnf_matrix = confusion_matrix(y_actual, y_pred, labels=[0, 1]) # confusion matrix 생성
# Non-normalized confusion matrix 그리기
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=[0, 1],
title='Confusion matrix, without normalization')
위에서 만들었던 plot_confusion_matrix 함수를 사용하여 confusion matrix를 시각화해보았습니다. 결과는 아래와 같습니다.
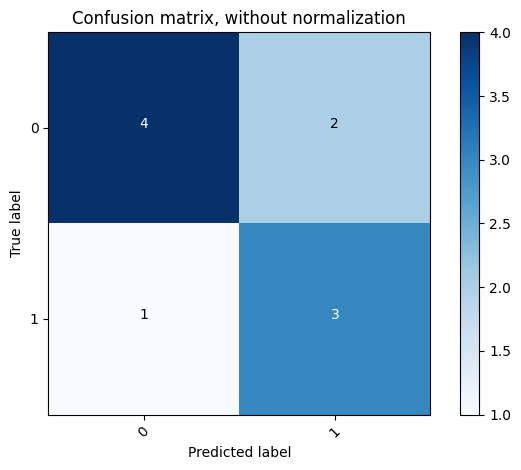
Seaborn 라이브러리를 이용하여 confusion matrix 시각화
처음에 언급드렸다시피, seaborn 라이브러리를 이용하면 훨씬 간단한 코드로 confusion matrix를 시각화할 수 있습니다.
import seaborn as sns
cnf_matrix = confusion_matrix(y_actual, y_pred, labels=[0, 1])
sns.heatmap(cnf_matrix, annot=True, cmap='Blues')
plt.xlabel('Predicted label')
plt.ylabel('True label')
plt.title('Confusion matrix, without normalization')
너무 간단하죠? 놀랍게도 이 짧은 코드의 결과가 위에서 길게 작성한 코드의 결과와 완전히 똑같이 나옵니다.

성능지표 확인
print('Accuracy =', accuracy_score(y_actual, y_pred))
print('Report = \n', classification_report(y_actual, y_pred))
'''
precision = TP / (TP + FP)
recall = TP / (TP + FN)
f1-score = 2 / (1/recall + 1/precision)
accuracy = (TP + TN) / (TP + FP + TN + FN)
support : 각 label의 실제 샘플 개수
macro avg : 모든 label에 대한 특정 성능 지표 값의 평균
weighted avg : 각 클래스에 속하는 표본의 개수로 가중 평균을 내서 계산 (샘플 개수 불균형 고려)
'''
accuracy_score() 함수를 사용하면 accuracy를 반환해줍니다.
classification_report() 함수를 사용하면 정말 많은 지표를 알려주는데요, 하나하나 뜯어 보도록 하겠습니다.
1. precision
: TP / (TP + FP)로 계산할 수 있으며, P로 예측한 것들 중에 맞춘 것의 비율이라는 의미를 갖습니다.
2. recall
: TP / (TP + FN)으로 계산할 수 있으며, 실제로 P인 것들 중에 맞춘 것의 비율이라는 의미를 갖습니다.
3. f1-score
: 2 / (1/recall) + (1/precision)으로 계산할 수 있으며, recall과 precision의 조화평균입니다.
4. support
: 각 label에 해당하는 실제 샘플의 개수를 의미합니다.
5. accuracy
: (TP + TN) / (TP + FP + TN + FN)으로 계산할 수 있으며, 전체 중에서 맞춘 것의 비율이라는 의미를 갖습니다.
6. macro avg
: 모든 label에 대한 특정 성능 지표 값의 평균을 의미합니다. 말이 좀 어렵죠? 예를 들어 보겠습니다.
=> 위 결과 표의 precision 열을 보시면 label이 0인 클래스는 0.80, 1인 클래스는 0.60입니다. 이 두 값의 평균을 구하면 (0.80 + 0.60) / 2 = 0.70이 됩니다. 즉, precision에 대한 macro avg는 0.70이 되는 것입니다.
7. weighted avg
: macro avg와 원리는 같지만, weighted avg는 각 클래스에 속하는 표본의 개수로 가중 평균을 내서 계산한다는 점에서 macro avg와 다릅니다. 샘플 개수의 불균형을 고려한 지표라고 볼 수 있겠습니다.
'Study > AI' 카테고리의 다른 글
| [AI] Artificial Intelligence 인공지능 입문 강의 (POSTECH 유환조 교수님) (0) | 2024.06.07 |
|---|---|
| [AI] CNN(Convolutional Neural Network)을 사용하여 MNIST 데이터 분류하기 (1) | 2024.04.10 |
| [AI] 로지스틱 회귀(Logistic Regression) 직접 구현하기 (0) | 2024.03.25 |
| [AI] 선형 회귀(Linear Regression) 직접 구현하기 (2) | 2024.03.25 |



