TensorFlow에는 자동 미분을 가능케 해주는 tf.GradientTape API가 있습니다.
이번 포스팅에서는 TensorFlow의 Gradient Tape를 활용하여 자동 미분 계산을 수행해보고, 그 과정을 수식으로 하나씩 풀어서 살펴보겠습니다.
Gradient Tape를 사용한 예제 코드
# 가중치(W)와 편향(b)
W = tf.Variable(tf.random.normal((3,2)), name ="wieghts")
b = tf.Variable(tf.zeros(2, dtype=tf.float32), name = "biases")
# 입력 데이터 (1x3)
x = [[1., 2., 3.]]
with tf.GradientTape() as tape:
y = x @ W + b # 선형 회귀 연산 (y = Wx + b)
loss = tf.reduce_mean(y**2) # 손실함수 (평균제곱오차)
# 미분 계산
dl_dW, dl_db = tape.gradient(loss, [W, b])
print(f"W.shape: {W.shape}, dW.shape: {dl_dW.shape}")
print(f"b.shape: {b.shape}, db.shape: {dl_db.shape}")
위 코드는 크게 아래와 같은 과정을 거칩니다.
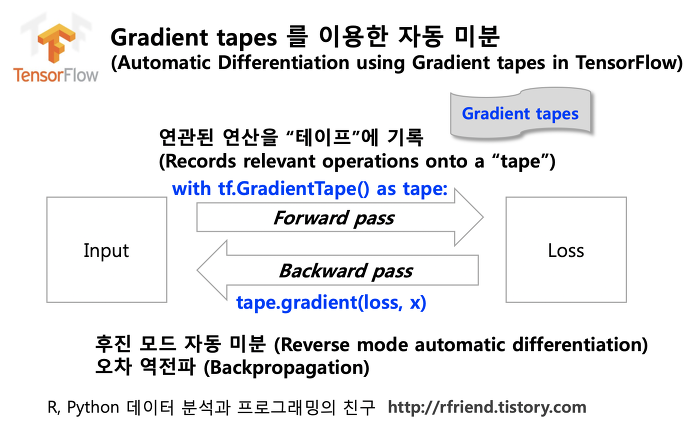
쉽게 말해, input이 들어오면, 설정한 함수를 통과(forward propagation)하고, 손실 함수를 가중치와 편향 각각에 대해 미분(back propagation)하여 손실 함수를 최소화하는 방향을 찾아낸다는 것입니다.
코드 해석
1️⃣ 변수 정의
# 가중치(W)와 편향(b)
W = tf.Variable(tf.random.normal((3,2)), name ="wieghts")
b = tf.Variable(tf.zeros(2, dtype=tf.float32), name = "biases")
# 입력 데이터 (1x3)
x = [[1., 2., 3.]]- W : (3,2) 크기의 가중치 행렬
- b : (2,) 크기의 편향 벡터
- x : (1,3) 크기의 입력 벡터
2️⃣ Forward Propagation 연산
y = x @ W + b # (1,3) x (3,2) = (1,2)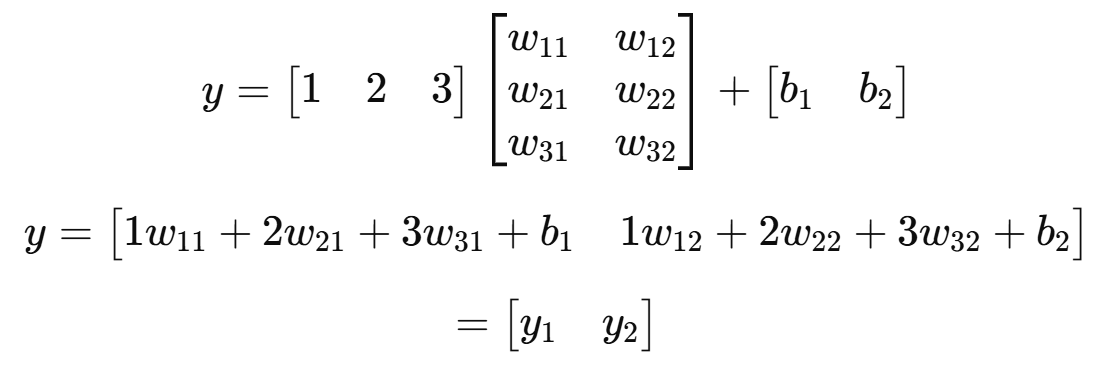
3️⃣ 손실 함수 (Loss) 정의
loss = tf.reduce_mean(y**2)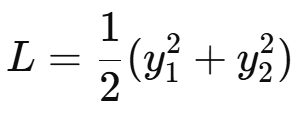
4️⃣ 역전파 (Backpropagation) - 미분 계산
dl_dW, dl_db = tape.gradient(loss, [W, b])
이제 손실 L을 가중치 W와 편향 b에 대해 미분하면, 가중치와 편향이 손실을 줄이는 방향을 찾을 수 있습니다.
(1) 가중치 W에 대한 미분
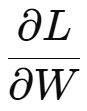
먼저, L을 W에 대해 미분하는 것을 어떻게 표현할 수 있을지 한번 유도해봅시다.
y를 W에 대해 미분해봅시다.
y = xW + b 에서 양변을 W에 대해 미분하면 아래와 같이 나오게 됩니다.
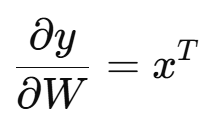
이것을 연쇄법칙을 사용한 식에 넣어볼까요?
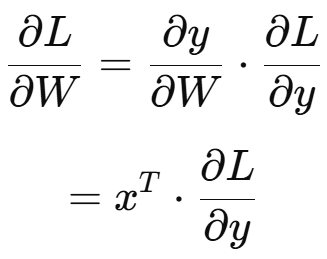
따라서 위 식은 아래와 같이 표현될 수 있습니다.
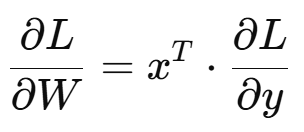
이제 손실을 y에 대해 미분한 값을 찾아야겠죠?
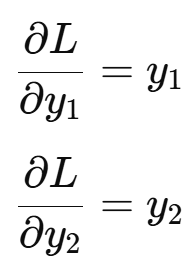
따라서,
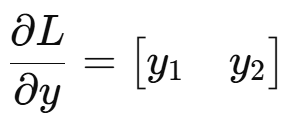
저는 x도 알고 y도 알기 때문에 이제 풀 수 있습니다.
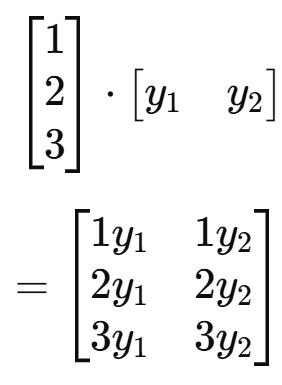
즉, dl_dW의 크기는 (3x2) 입니다.
(2) 편향 b에 대한 미분
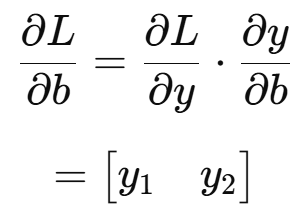
제가 설정한 선형 회귀 식의 경우, y를 b에 대해 미분하면 1이므로, 연쇄 법칙에 대입하면 L을 y에 대해 미분한 결과와 같은 결과가 나오게 됩니다.
즉, dl_db의 크기는 (1×2) = (2,) 입니다.
결론 정리
- W.shape → (3,2)
- dl_dW.shape → (3,2), 입력값 x 와 출력값 y 를 사용하여 계산됨
- b.shape → (2,)
- dl_db.shape → (2,), 출력값 y 와 동일한 크기를 가짐
'Study > AI' 카테고리의 다른 글
| [AI] 배치 정규화(Batch Normalization)란? (0) | 2025.02.07 |
|---|---|
| [AI] GAN(Generative Adversarial Networks)에 대하여 (1) | 2025.02.06 |
| [AI] TensorFlow 기초 개념과 활용 (0) | 2025.02.06 |
| [AI] CNN(Convolutional Neural Networks)에 대하여 (0) | 2025.01.27 |



