선형대수학을 공부하다보면 Ax=0라는 형태의 식을 많이 접하게 되는데요,
이걸 기하학적으로 이해하지 못하고 그냥 계산기처럼 수식 계산만 하게되면 선형대수학을 공부하는 의미가 없어집니다.
제가 그랬죠... 그래서 다시 공부하는 중...
그러니까 Null space에 대해 정확하게! 직관적으로! 한번 살펴보자구요!
Null Space의 수학적 정의
Null Space(영공간)는 선형대수에서 다음과 같이 정의됩니다.
어떤 행렬 A가 있을 때, $A\overrightarrow{x} = \overrightarrow{0}$를 만족시키는 모든 벡터 $\overrightarrow{x}$의 집합
즉, 행렬 A에 곱했더니 결과가 0이 되는 x들만 모은 공간을 말하는 것이죠.
Null Space의 직관적 예시
아래와 같은 Ax=0 형태의 식이 있다고 해봅시다.
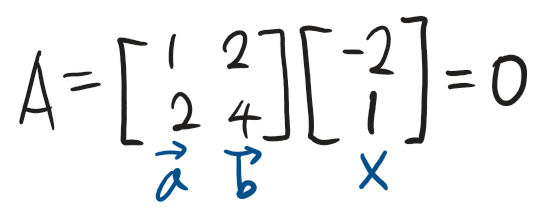
이걸 다시 풀어서 표현해보면 이렇게 되겠죠?

자 그럼 이걸 좌표 평면으로 가져가보겠습니다.

어떤가요?
$\overrightarrow{a}$와 $\overrightarrow{b}$는 선형 종속으로, 2차원 공간을 형성하지 못하고 있습니다.
1차원 공간인 직선만 만들어내고 있죠.
이 vector space를 0으로 만드는 벡터는 바로 $\overrightarrow{a}$와 $\overrightarrow{b}$가 만들어내고 있는 공간에 정확히 수직인 벡터 $\overrightarrow{x}$가 됩니다.
바로 이 벡터 $\overrightarrow{x}$가 만드는 공간이 Null Space가 되는 것입니다!
놀랍지 않나요?
이 개념을 이해하고 선형대수학의 모든 수식을 바라본다면 더 넓게 학문을 바라볼 수 있겠죠!
'Study > Linear Algebra' 카테고리의 다른 글
| [Linear Algebra] Matrix(행렬)은 Linear Operator(선형 연산자)이다? (0) | 2025.05.19 |
|---|---|
| [Linear Algebra] 선형 독립(Linear Independence)과 기저(Basis) (0) | 2025.05.18 |
| [Linear Algebra] 데이터의 차원 (0) | 2024.08.12 |


