공부를 하다보면 행렬을 단순히 숫자 더미로 생각하게 될 때가 있는데요, 그러면 우리 뇌는 그냥 본질을 내다버린 계산기가 되어 버립니다. 제가 그랬어요..ㅠㅠ
그래서! 우리는 반드시 이 행렬이라는 녀석이 벡터를 변형하는 구조적 도구라는 걸 이해하고 선형대수를 바라보아야 합니다.
그래야 선형대수라는 학문을 훨씬 더 입체적으로 볼 수 있게 됩니다.
Linear Operator(선형 연산자)란?
먼저 선형 연산자가 무엇인지부터 알아야 되겠죠?
선형 연산자는 말 그대로 벡터를 입력받아 다른 벡터로 바꾸는 함수입니다. 그런데 조건이 하나 있어요.
어떤 함수 $T$가 선형 연산자가 되려면, 다음 두가지를 만족해야 합니다.
1. 덧셈 보존 (Additivity)
$$T(\overrightarrow{u} + \overrightarrow{v}) = T(\overrightarrow{u}) + T(\overrightarrow{v})$$
2. 스칼라 곱 보존 (Homogeneity)
$$T(c\overrightarrow{v}) = cT(\overrightarrow{v})$$
즉, 벡터 공간의 구조를 유지하면서 작동하는 함수라는 뜻입니다.
왜 행렬이 선형 연산자일까?
아래와 같은 식이 있다고 해봅시다.
2x2 행렬에 벡터를 곱한 형태입니다.

결과를 보시면, 행렬에 벡터를 곱했는데 벡터가 나오고 있습니다.
즉, 행렬은 하나의 벡터를 어떤 새로운 벡터로 바꿔주는 연산자처럼 작동하고 있는 것이죠!
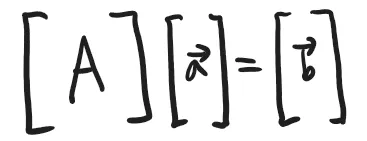
그리고 직접 확인해보시면, 이 연산은 위에서 언급한 선형 연산자 조건을 항상 만족합니다.
- $A(\overrightarrow{u} + \overrightarrow{v}) = A\overrightarrow{u} + A\overrightarrow{v}$
- $A(c\overrightarrow{v}) = cT(\overrightarrow{v})$
따라서, 행렬은 선형 연산자라고 볼 수 있습니다!
선형 연산자로서의 행렬의 기하학적 의미
위에서 사용했던 식을 다시 들고와보겠습니다.

여기서 $x_1 = 1$, $y_1 = 1$라고 해봅시다.
그러면 아래와 같이 벡터가 선형 변환되는 것을 확인할 수 있죠.
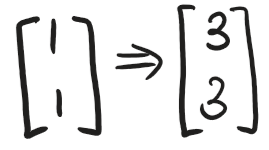
이게 좌표계에서 어떤 의미를 지니는지 확인해봅시다.

노란색은 원래 좌표계, 연두색은 곱해진 행렬이 이루는 vector space입니다.
이렇게 행렬은 공간을 비틀 수 있는데요, 기존에 (1, 1) 좌표는 비틀어진 공간에서 (3, 3)으로 매핑되는 것입니다.
다시 말해, 행렬에 벡터를 곱한다는 것은 해당 행렬이 만드는 새로운 좌표축에 벡터를 매핑시킨다는 것을 의미합니다.

더 구체적으로는, 곱한 벡터에 대해 변환된 좌표계에서의 위치를 원래 좌표계에서 표현하는 좌표값으로 변환해주는 것이지요!
'Study > Linear Algebra' 카테고리의 다른 글
| [Linear Algebra] Null Space(영공간)에 대하여 (0) | 2025.05.18 |
|---|---|
| [Linear Algebra] 선형 독립(Linear Independence)과 기저(Basis) (0) | 2025.05.18 |
| [Linear Algebra] 데이터의 차원 (0) | 2024.08.12 |


