데이터 분석에서 고차원 데이터는 때때로 분석을 복잡하게 만들고, 모델 성능을 저하시킬 수 있습니다.
이를 해결하기 위한 강력한 도구 중 하나가 바로 주성분 분석(PCA)입니다.
이번 포스팅에서는 PCA의 개념과 필요성을 이해하고, Python을 사용한 구현 방법을 알아보겠습니다.
주성분 분석(PCA, Principal Component Analysis)이란?
PCA란 고차원 데이터를 저차원으로 축소하면서 데이터의 분산(정보)를 최대한 보존하는 선형 차원 축소 기법입니다.
- 데이터를 새로운 좌표계로 변환하여 데이터의 주요 패턴을 찾고, 불필요한 차원을 제거하는데 사용합니다.
예) 3차원의 데이터를 2차원의 주성분 공간으로 사영(projection)시키면 원래 데이터가 가지고 있는 특징의 대부분이 보존
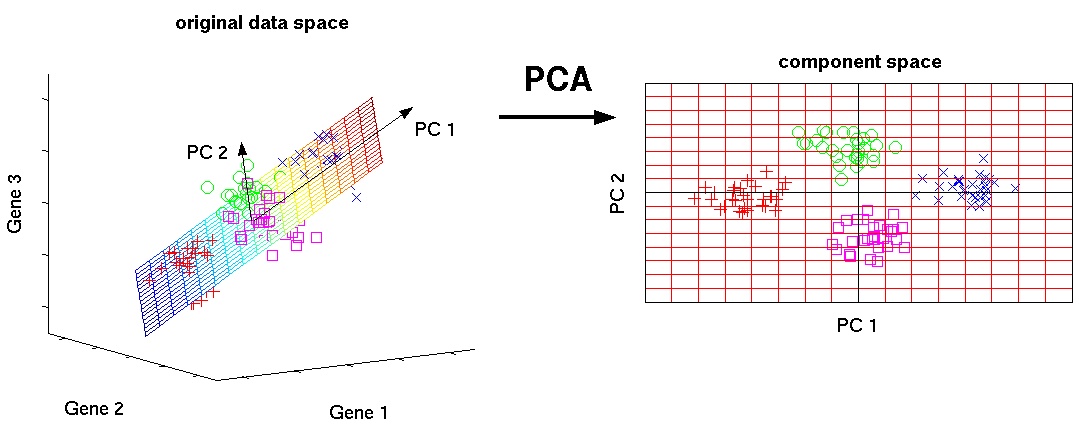
PCA가 필요한 이유
1. 고차원 데이터 문제 완화
- 고차원 데이터는 차원의 저주(Curse of Dimensionality) 문제를 유발합니다. 이 문제는 데이터가 차원이 증가할수록 희소해지고 분석이 어려워지는 현상을 말합니다.
2. 시각화
- 고차원 데이터를 2D 또는 3D로 변환하여 시각화할 수 있습니다.
3. 모델 성능 개선
- 노이즈를 줄이고, 주요 특징만 남겨 모델 학습 성능을 개선할 수 있습니다.
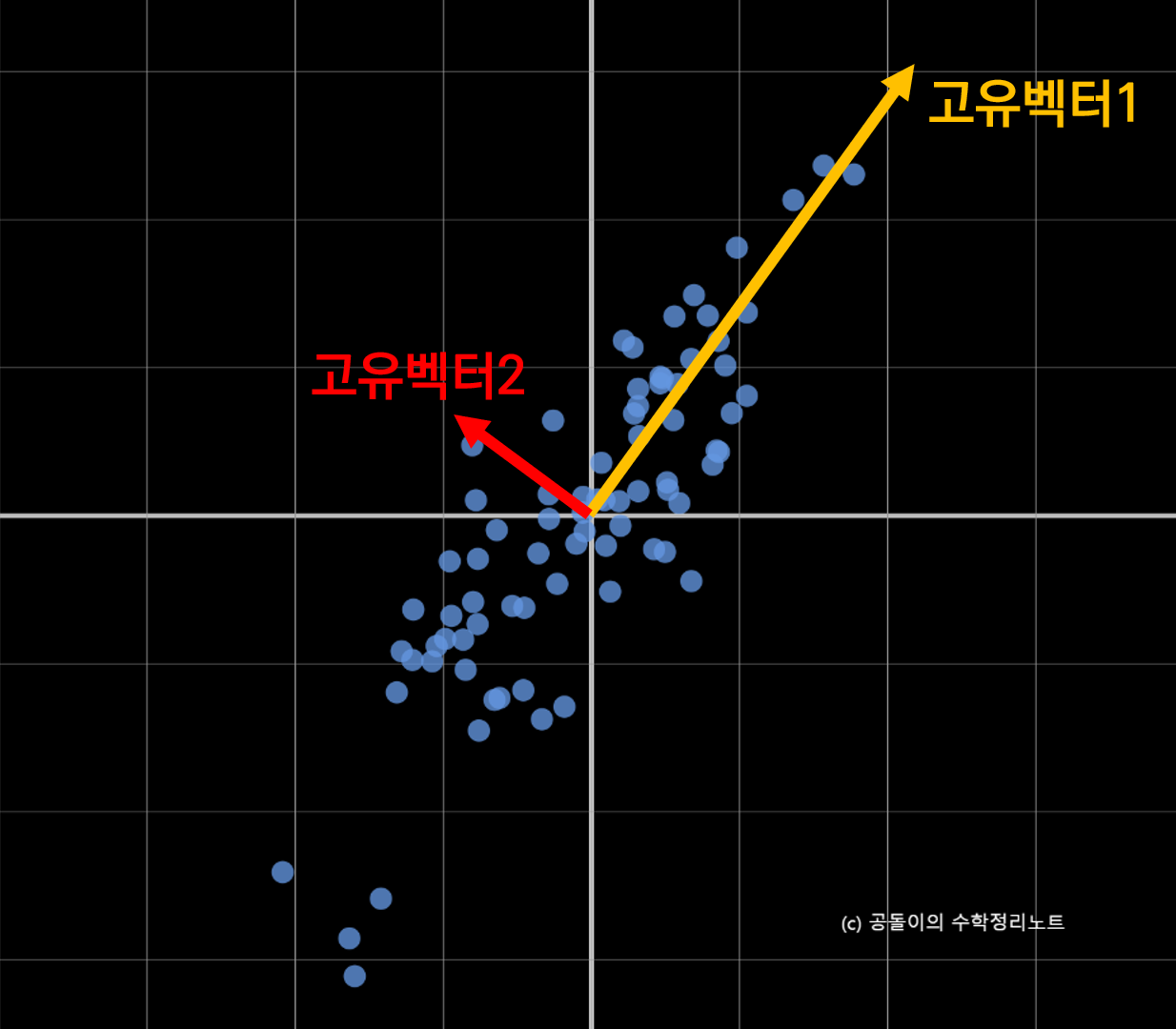
PCA의 원리 - 주성분(Principal Component)

- 데이터의 분산이 가장 큰 방향을 나타내는 새로운 축
- PC1(1번째 주성분): 데이터 분산이 가장 크게 설명하는 축
- PC2(2번째 주성분): PC1에 직교하면서 분산이 그 다음으로 큰 방향

PCA의 원리 - 공분산 행렬(Covariance Matrix)
- 데이터의 변수들 간의 관계를 나타내는 공분산 행렬
- 공분산 행렬의 고유값과 고유벡터를 사용해 주성분을 정의
- 고유값이 큰 순서대로 고유벡터를 정렬하면 중요한 주성분을 구할 수 있음

- 고유값(Eigenvalue): 주성분이 설명하는 분산의 크기
- 고유벡터(Eigenvector): 주성분의 방향
PCA의 과정
PCA는 데이터를 단순화하고 중요한 특징만 남기기 위해 아래 5단계 과정을 거칩니다.
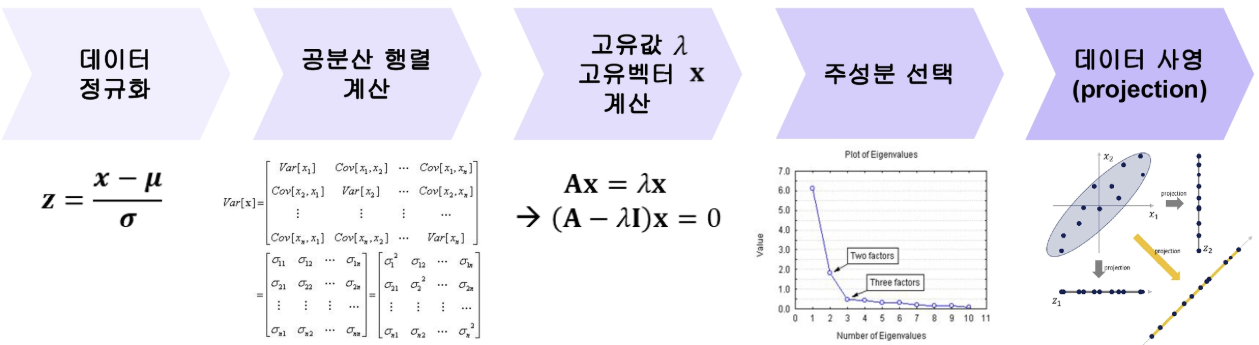
1단계: 데이터 정규화
데이터의 크기 차이가 너무 크면 PCA의 결과에 영향을 미칠 수 있습니다. 이를 해결하기 위해 데이터를 정규화(표준화)합니다.

- x: 원본 값
- μ: 평균
- σ: 표준 편차
정규화를 통해 모든 변수의 평균을 0, 표준 편차를 1로 맞춰줍니다.
2단계: 공분산 행렬 계산
변수 간의 상관관계를 나타내는 공분산 행렬을 계산합니다.
- 공분산은 두 변수 간의 변화 관계를 나타냅니다. 값이 클수록 두 변수가 강하게 연관되어 있다는 뜻입니다.
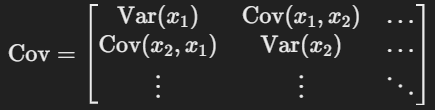
3단계: 고유값과 고유벡터 계산
공분산 행렬에서 고유값(λ)과 고유벡터(x)를 계산합니다.
- 고유값: 각 주성분이 데이터를 얼마나 잘 설명하는지를 나타냅니다.
- 고유벡터: 주성분의 방향을 나타냅니다.
특성 방정식을 풀어서 고유값과 고유벡터를 구합니다:
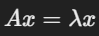
- A: 공분산 행렬
- x: 고유벡터
- λ: 고유값
4단계: 주성분 선택
고유값이 큰 순서대로 주성분을 선택합니다. 일반적으로, 전체 분산의 95% 이상을 설명하는 주성분만 선택합니다.
- 고유값이 클수록 해당 주성분이 데이터를 더 잘 설명합니다.
- Scree Plot(스크리 플롯)을 사용해 몇 개의 주성분을 선택할지 결정합니다. 그래프에서 "기울기가 완만해지는 점"을 기준으로 주성분 개수를 정합니다.
5단계: 데이터 사영(Projection)
선택한 주성분 축으로 데이터를 투영(projection)합니다.
- 원래 데이터는 고차원 공간(예: x1,x2,x3x_1, x_2, x_3)에 존재하지만, 주성분 축(예: z1,z2z_1, z_2)으로 투영하면 데이터가 저차원으로 변환됩니다.
- 이를 통해 차원을 줄이면서도 중요한 정보를 유지할 수 있습니다.
PCA 구현 (Python)
(1) 데이터 준비
데이터 셋 : Adult Census Income
Adult Census Income
Predict whether income exceeds $50K/yr based on census data
www.kaggle.com
(1) 데이터 표준화
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train = pd.DataFrame(scaler.fit_transform(X_train), columns = X.columns)
X_test = pd.DataFrame(scaler.transform(X_test), columns = X.columns)- 문제
- 데이터의 변수들(특성들)이 서로 다른 단위나 범위를 가지는 경우, 값의 크기가 큰 변수가 모델 학습에 더 큰 영향을 미칠 수 있음
- 결과적으로, 크기 차이가 큰 변수에 의해 모델이 왜곡될 가능성이 있음
- 해결
- 표준화를 통해 변수의 평균을 0, 분산을 1로 맞춤으로써 동일한 스케일로 변환됨
- 변수 간 크기 차이가 모델 학습에 미치는 영향을 제거함
(2) PCA 적용
from sklearn.decomposition import PCA
# PCA 진행
pca = PCA()
X_pca = pca.fit_transform(X_train)
X_test_pca = pca.transform(X_test) # Test 데이터에도 동일한 PCA 적용- fit_transform: 훈련 데이터셋에 PCA를 학습(fit)하고, 데이터를 주성분 축으로 변환(transform)
- transform: 테스트 데이터셋을 PCA로 변환(학습된 PCA를 그대로 사용)
(2) PCA 결과 데이터프레임 만들기
# PCA 데이터 프레임 생성
pca_df = pd.DataFrame(X_pca, columns=[f"PC{i+1}" for i in range(X_pca.shape[1])])
pca_test_df = pd.DataFrame(X_test_pca, columns=[f"PC{i+1}" for i in range(X_test_pca.shape[1])])
pca_df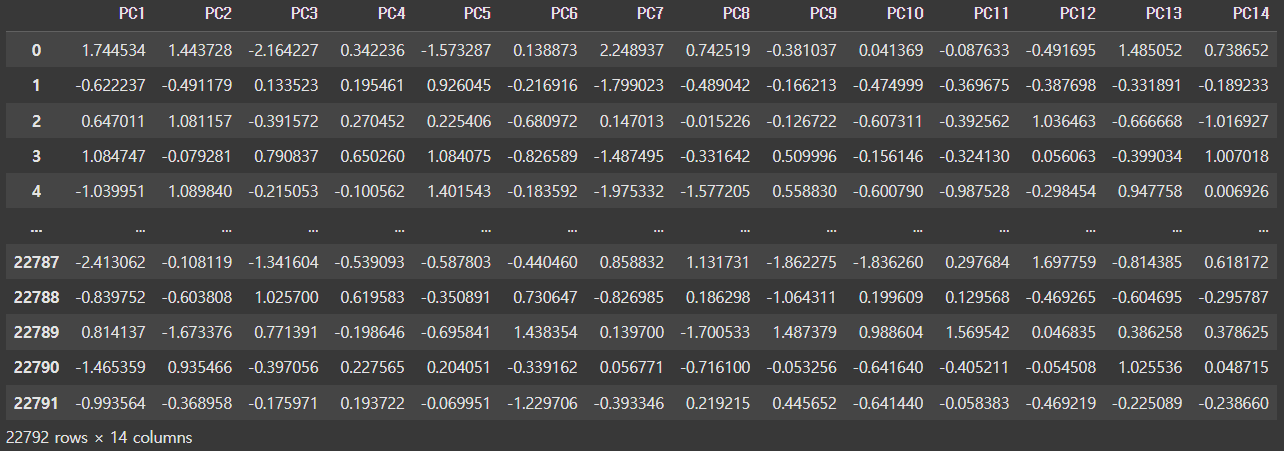
(3) 각 주성분이 설명하는 분산 비율 데이터프레임 만들기
# 각 주성분이 설명하는 분산 비율
explained_variance = pca.explained_variance_ratio_
# 설명된 분산 비율을 데이터프레임으로 저장
explained_variance_df = pd.DataFrame({
"Principal Component": [f"PC{i+1}" for i in range(len(explained_variance))],
"Explained Variance Ratio": explained_variance
})
explained_variance_df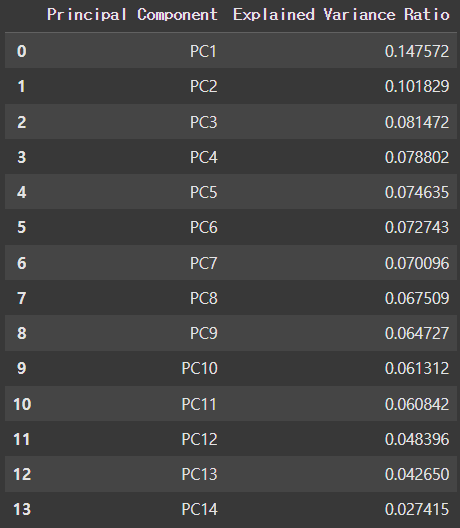
- pca는 원래 데이터의 컬럼을 조합하여 만든 새로운 축(Principal Component)을 의미함
- 각 축은 데이터의 분산을 최대화하는 방향으로 정의되며, 축의 순서는 데이터의 분산이 큰 순서대로 정렬됨
(4) 로딩 매트릭스(Loading Matrix) 계산
PCA의 로딩 매트릭스는 원래 변수와 주성분 간의 상관관계를 나타냅니다.
# 로딩 매트릭스 계산
loading_matrix = pd.DataFrame(
pca.components_.T,
columns=[f"PC{i+1}" for i in range(pca.components_.shape[0])],
index=X_train.columns
)
loading_matrix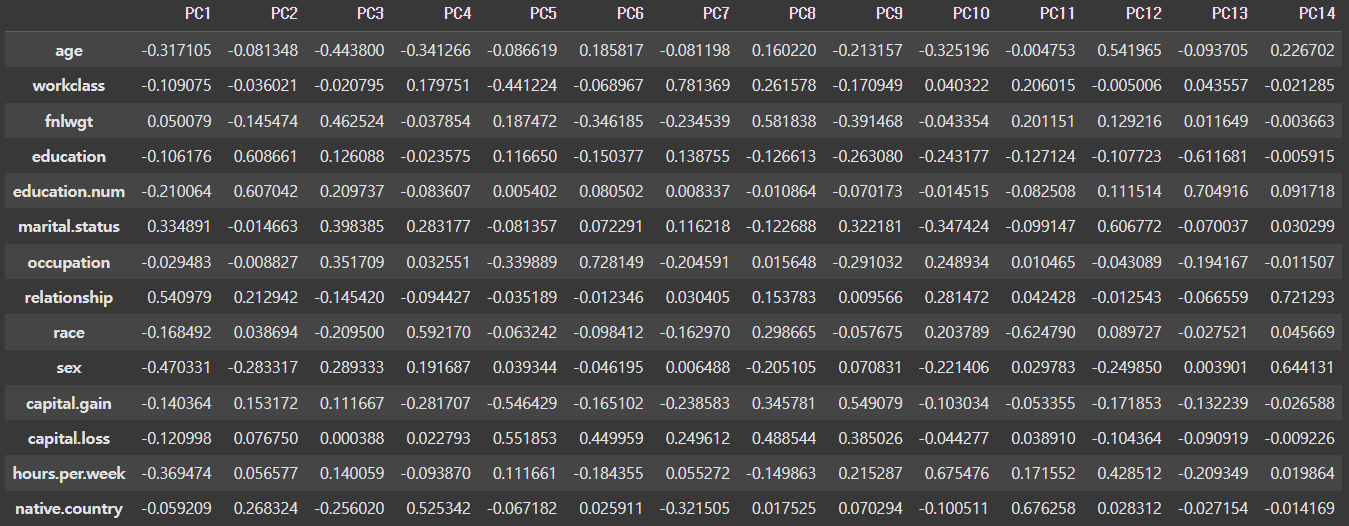
- loading matrix는 각 주성분이 원래 컬럼에 대해 얼마나 영향을 받는 지 알 수 있음
- 로딩값의 절대값이 클수록 해당 특성이 주성분에 미치는 영향이 크며, 주성분을 형성하는 데 중요한 역할을 함
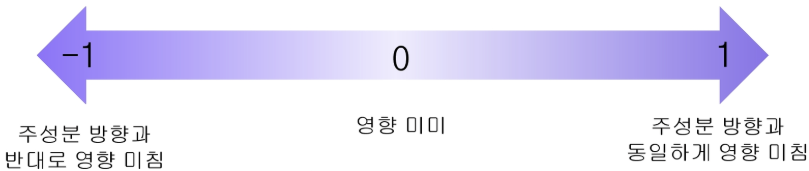
즉, 우리는 로딩 매트릭스를 통해 어떤 변수가 주성분에 가장 큰 영향을 미치는지 확인할 수 있습니다!
(5) PCA 결과 시각화
- PCA를 통해 각 주성분이 데이터의 분산을 얼마나 설명하는지 분석한 결과를 토대로 누적 분산 비율(Cumulative Variance Ratio)을 구하면, 이를 기준으로 적절한 주성분의 개수를 선택할 수 있습니다.
- 일반적으로 누적 분산 비율이 80~95%이면 원래 데이터의 주요 패턴을 대부분 유지한다고 판단할 수 있습니다.
# 데이터의 변동성 비율 누적값
cumulative_variance = explained_variance_df["Explained Variance Ratio"].cumsum()
plt.figure(figsize=(10, 6))
# Bar plot
plt.bar(explained_variance_df["Principal Component"],
explained_variance_df["Explained Variance Ratio"],
color='skyblue', edgecolor='black', label='Individual Explained Variance')
# 데이터의 변동성 비율 누적값 Line plot
plt.plot(explained_variance_df["Principal Component"],
cumulative_variance,
color='orange', marker='o', label='Cumulative Explained Variance')
plt.title('PCA', fontsize=16)
plt.xlabel('Principal Component', fontsize=12)
plt.ylabel('Explained Variance Ratio', fontsize=12)
plt.xticks(fontsize=10)
plt.yticks(fontsize=10)
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.legend(fontsize=12)
# Show the plot
plt.show()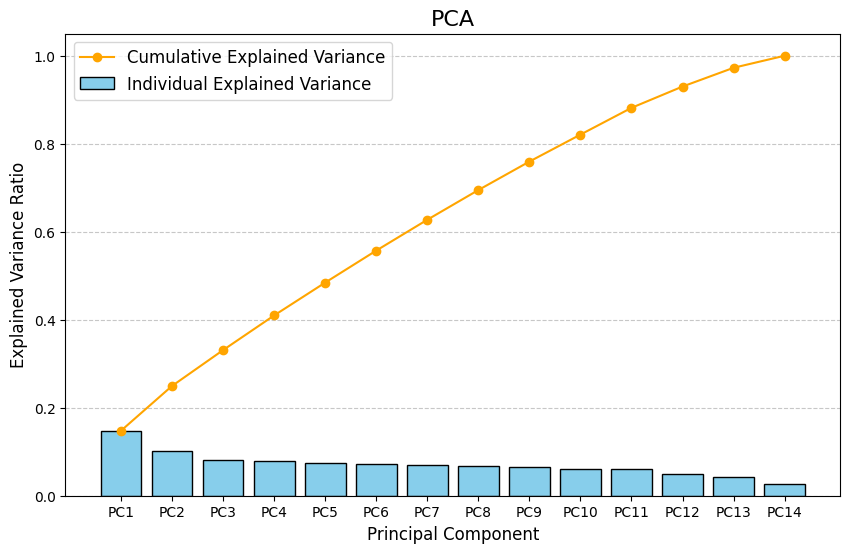
- 여기서는 PC1~PC11까지 누적 분산 비율이 약 80~90% 사이이기 때문에 데이터의 주요 정보를 효율적으로 유지하면서 차원을 축소할 수 있습니다.
- 나머지 주성분(PC12~14)은 설명하는 분산 비율이 낮아, 모델 성능에 거의 영향을 미치지 않는다고 판단할 수 있습니다.
PCA의 한계
1. 정보 손실
- 차원을 축소하는 과정에서 일부 정보가 손실될 수 있습니다. 주성분이 데이터를 잘 설명하는지 항상 확인해야 합니다.
2. 선형성 가정
- PCA는 데이터가 선형적으로 관계되어 있다고 가정합니다. 비선형 데이터에는 다른 기법(t-SNE, UMAP)을 고려할 수 있습니다.
3. 해석의 어려움
- 축소된 주성분은 원래 변수의 선형 조합이기 때문에, 주성분 자체의 해석이 어려울 수 있습니다.
'Study > Data Science' 카테고리의 다른 글
| [Data Science] Feature 선택 및 중요도 평가 (1) | 2024.12.08 |
|---|---|
| [Data Science] Feature(차원) 축소 - t-SNE(t-Distributed Stochastic Neighbor Embedding) (0) | 2024.12.07 |
| [Data Science] Feature Selection - 유전 알고리즘(Genetic Algorithm, GA) (0) | 2024.12.07 |
| [Data Science] 결측 데이터 처리 방법 (3) | 2024.12.06 |



